Sageの使い方(入口)¶

櫻川貴司

この資料では数学ソフトウェアであるSage(セイジ。SageMathと記すこともある)について簡単に説明しています。

以下の説明はnotebook環境であるJupyterの使い方についてある程度知っていることを前提としています。またプログラミング言語Pythonについては知っている方が有利ですが、この資料では必ずしもそれを前提としていません。元々はSageのversion8に基づいて説明していたものを、改訂してversion9対応に書き直したものです。もしも正しくない箇所がありましたらご指摘いただきますと助かります。 8より前の場合、notebook形式がSage独自のものでした。 8以降ではJupyterが標準となります(8では従来のものも利用可能です)。ここではほとんどJupyterを利用する場合を説明しています。

北米やEUの一部の国では高等学校までや大学の数学教育に日本よりも電卓を積極的に取り入れており、数式処理・グラフ表示・プログラミングができる電卓の機種が豊富で、日本よりも多く販売されていたりします。機能が規定内なら試験にも持ち込み可だったりします。具体的にはTI Nspire CX CAS、HP Prime、CASIO fx-CP400などは数式処理を行えます(現在機種が多いのはTI。但しこういった電卓は試験持ち込み制限がある場合があります)。フランスでは、高校でPythonのプログラミングを教えることになるためか、 CASIOやTIは(micro-)Pythonが動く電卓のファームウェアや外部拡張機器を出す、あるいは出す予定があるようです。 CASIOは北米販売用の電卓でもmicro-Pythonが動作するファームウェアを出していますが、ハードウェア的にはほとんど同じと思われる国内販売のグラフ電卓用には今の所出していません。

日本では事情は異なり、数学教育を担っている先生達(特に教育審議会の関係者)の大部分は上記の国のような教育方針には現在はあまり賛成しないように思えます。確かにどちらがよいかは一長一短だと考えられます。しかし、いわゆる文科系の大学でも入試等や入学後に数学を必須にするという意見があちこちで出てきているなど、数学教育を満遍なく受けられるようになってゆく可能性があります。また、いわゆるデータサイエンスや統計的な技法もかなりの分野で今後ますます必要とされてゆくでしょう。そういう方向性で教育内容を変更してゆくと、教員の能力を考慮すべき実現可能性の議論は別として、 PCあるいは電卓によるグラフ表示や数式処理を今よりずっと積極的に授業で用いるのが望ましいという意見が優勢となる可能性があると考えられます。

数学の原理的な部分を理解することと、数学を実用的なことに応用することは全く同じではありません。後者の場合にはPCや電卓の積極的な利用が有用な場合が結構あります。前者の場合にも数学的な現象を視覚化することで理解が深まる場合がありますし、数式処理等が役立つことがあります。数学者が数値計算や数式処理を研究に役立てている場合も多いです。

Sageの日本語の文献の一部¶

最近はgoogle翻訳やDeepLの機能の一部が制限付きで無料で使用可能であり、外国語文献の日本語翻訳を作ることが容易になっています。かなりこなれた翻訳が可能になっているとはいえ、現状ではPDFファイルの翻訳では式などが乱れて読めなくなるなどの欠点があります。

オンラインで利用できる数式処理システム¶

少々試す程度であればメールアドレスによる登録なしで利用できるようなオンラインの数式処理システムがいくつかあります。

Sageのインストール¶

BYODのPCの場合にはSageをインストールする必要があります。 Sageのサイトやインストールガイドを参照してインストールします。ダウンロード後のウィルススキャンを忘れずに行なってください。

但し、anacondaなど他のPythonを利用する環境と同時にインストールする場合には、競合したりしてうまく動作しない可能性が出てきます。そのような場合には、pyenvやconda等を利用してアプリケーションごとに環境を分けるようにすれば解決できると考えられます。こうする場合、インストールや環境管理にはGUIを利用せずにコンソール(Windowsの場合コマンドプロンプト)ベースでCUIで行うことになる場合がほとんどでしょう。このパラグラフ内の記述はこの資料が対象とする技術的な水準を超えていると思われますし、短くは説明できません。必要があり、やる気がある人は自分で調べてそのようにしてください。質問があれば対応します。

Sageの起動方法¶

GUIによりSageをインストールしてある場合、通常のアプリケーションの一つとしてGUIにより起動します。しばらく待つとJupyter notebookのページがwebブラウザに表示されます。例えばWindowsの場合にはスタートメニューからメニュー階層を辿って起動します。表示はSageMathとなっている場合が多いです。 Jupyter notebookを利用する言語が他にある場合、別の方法でJupyter notebookを起動しておけばNewメニューにSageMathが現れ、選択できることがあります。もしそうであればそのようにしても利用できます。 CUIでインストールした場合には通常CUIでコンソールから起動することになります。

以下では上から順番にCodeのセルを実行することを前提にしています。順序を変えると結果が異なる場合やエラーとなる場合があり得ます。

Jupyter notebookとしての利用¶

Jupyter notebookとしての利用方法はそちらの説明を読んでください。

教育環境によってはnotebookの保存先が普段使わないディレクトリになっている場合があります。そのような場合にはnotebookのダウン/アップロードを行えばよいでしょう。

Version表示¶

version()    # Sageのバージョンを表示する。

'SageMath version 9.6, Release Date: 2022-05-15'

実数計算(一部複素数)¶

Jupyterのセル(文章あるいはプログラムを入力する枠で囲まれた個別の領域)にSageの式やプログラムを入力し、セルの種別はCodeに設定します。Shift-return(enter)で式の値を求める/プログラムの実行を行います。以下に例を示します。

3+5*2/3 # の後はコメントとなる。

19/3

show(3+5*2/3)    # showという函数に与えると通常の数学の形式で表示する。

そのまま入力した場合には分数(有理数)計算となることに注意してください。分数表示等の数式表示の$\mathrm{\LaTeX}$形式を得たい場合には、表示の上で右クリックし(Macの場合は2本指タップ等)、 Show Math AsのTeX Commandsを選択します。数式表示にMathJaxというシステムを利用している場合にある程度共通する方法です。複雑な式の場合に特に有用です。

小数で演算結果を求めるには例えば以下のようにする方法があります。式の一部に浮動小数点数を含めて自動的に強制的なデータ型の変換(coercion)を行うか、函数nで変換します。

3.0+5*2/3

6.33333333333333

n(3+5*2/3)

6.33333333333333

虚数も取り扱えます。通常の数学での$i$の代わりにIを使います。 2つ目の例は、通常の数学の形式で表示させたいときに使う別の方法です。この場合にはshowの引数にしてもどちらでもうまく表示されます。これはPythonのオブジェクト指向の書き方を利用して、 show()というメッセージを数式のオブジェクトに送ることで表示を行なっていると考えられます。 Pythonを知らなくても(式).show()という書き方を知っていれば使えると思います。ただし、(式).show()という書き方は左側のオブジェクトの種類によってはエラーとなるので、その場合にはshow(式)という形式を試してください。

(2+I)*I

2*I - 1

show((2+I)*I)

既定義の函数(組み込み函数)・記号が色々あります。なお以下では2つの式を1つのセルの中に入れて実行していることに注意してください。ここでは単に表示領域を節約するためにそうしています。

show(factorial(6))    # この場合.show()を付けるとエラーになる。
factorial(300)        # こちらはshow()を付けていないがセル中の最後の式なので結果が表示される。

306057512216440636035370461297268629388588804173576999416776741259476533176716867465515291422477573349939147888701726368864263907759003154226842927906974559841225476930271954604008012215776252176854255965356903506788725264321896264299365204576448830388909753943489625436053225980776521270822437639449120128678675368305712293681943649956460498166450227716500185176546469340112226034729724066333258583506870150169794168850353752137554910289126407157154830282284937952636580145235233156936482233436799254594095276820608062232812387383880817049600000000000000000000000000000000000000000000000000000000000000000000000000

Sageでは記号として計算を行えるため、以下のように$\sin(\pi)$等の結果が正確に求まります。但しこれは最近の函数電卓やグラフ電卓の一部でもやはりそうなります。

sin(pi)

0

show(tan(pi/2))

説明と補完¶

函数名・記号名の前後に?を付けて実行すると説明がページ下部に出ます。

sin?

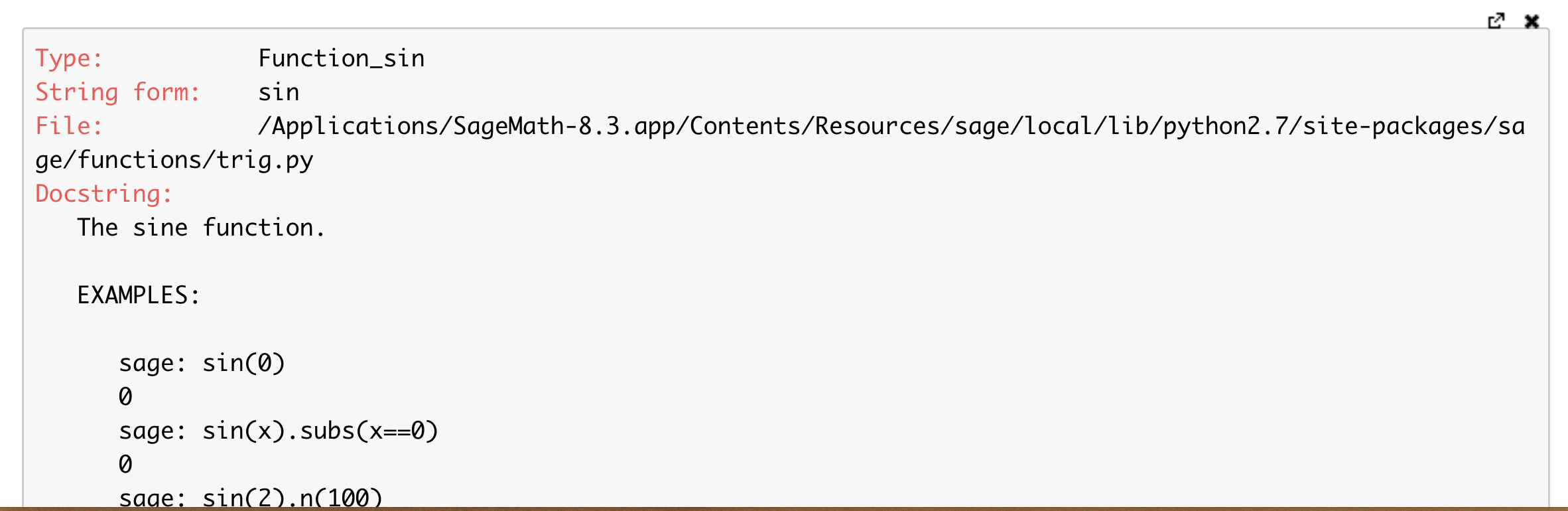
sage-function-explanation

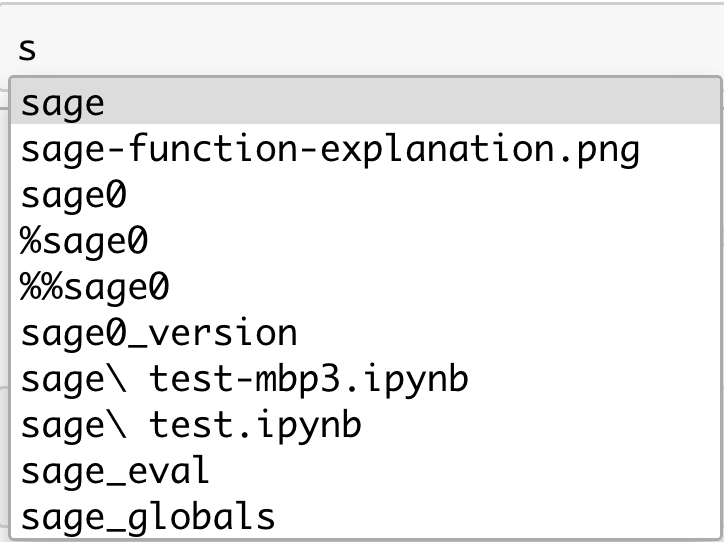
セルに函数名の文字列を途中まで打ち込んで[TAB]キーを押すと、その文字列から始まる函数やファイル名のリストから成るメニューが表示され、選択することができます。例えばsを打ち込んだ後で[TAB]を押してみてください。ただし、名前が一意的に特定される場合には、メニューが表示される代わりに特定された文字列が補完されます。

s

変数に値を入れて記憶させておくことができます。ここでの変数cはプログラム(Python)の変数で、後述の総和や代数式を扱う場合に式中に現れる記号変数とは扱いが異なりますので注意してください。

実数計算の続き¶

c=sin(pi/4)
c.show()

(c*c).show()

小数表現を得たければ以下のようにします。

c.n()

0.707106781186548

総和を求めることも可能です。

X=sum(x^2,x,0,100,hold=true)     # hold=trueにより、値を計算せずに総和の式のままとなる。
show(X,' =',X.simplify_full())   # simplify_fullにより、式を単純化する。showで3つの引数を順に表示する。
sum(x^2,x,0,100)                 # hold=trueを指定しなければそのまま計算する。

338350

ただし次のように入力するとエラーとなります。これはbが記号変数であるとSageが認識していないためで、その次のセルのようにすればそれ以降はbを記号変数として取り扱います。記号変数はPythonの変数とは異なります。それが式中に現れると、いわゆる数式の変数として扱われます。 xについては特別扱いで、最初から記号変数となっています。

sum(b^2,b,0,100)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
/var/folders/zc/9ttwyr_118101rcgsyd6kgq00000gp/T/ipykernel_14851/148545459.py in <cell line: 1>()
----> 1 sum(b**Integer(2),b,Integer(0),Integer(100))

NameError: name 'b' is not defined

var('b')    # bは記号変数である

b

sum(b^2,b,0,100)

338350

X=product(x,x,1,6,hold=true)    # 積の計算。展開しない式(hold=true)にしている
show(X,' =',X.simplify_full())  # simplify_fullで式を単純化している

多桁の円周率。

numerical_approx(pi, prec=1000)

3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127

プログラム¶

Pythonに似た文法でプログラムを記述することが可能です。ただし本稿ではPythonを知っていることを前提としていないので、プログラムについてはあまり説明しません。しかしなんとなくわかる部分はあるでしょうし、それでも十分です。 Pythonプログラムの部分が分からなければそこは飛ばしても構いません。

a=0                     # 変数aに0を代入する
for i in range(0,101):  # iの値を0から101の直前まで変えつつ繰り返す
    a=a+i               # aの値をi増やす
    print(i,a,',',end="")      # iとaを出力する。end=""は改行させないため

0 0 ,1 1 ,2 3 ,3 6 ,4 10 ,5 15 ,6 21 ,7 28 ,8 36 ,9 45 ,10 55 ,11 66 ,12 78 ,13 91 ,14 105 ,15 120 ,16 136 ,17 153 ,18 171 ,19 190 ,20 210 ,21 231 ,22 253 ,23 276 ,24 300 ,25 325 ,26 351 ,27 378 ,28 406 ,29 435 ,30 465 ,31 496 ,32 528 ,33 561 ,34 595 ,35 630 ,36 666 ,37 703 ,38 741 ,39 780 ,40 820 ,41 861 ,42 903 ,43 946 ,44 990 ,45 1035 ,46 1081 ,47 1128 ,48 1176 ,49 1225 ,50 1275 ,51 1326 ,52 1378 ,53 1431 ,54 1485 ,55 1540 ,56 1596 ,57 1653 ,58 1711 ,59 1770 ,60 1830 ,61 1891 ,62 1953 ,63 2016 ,64 2080 ,65 2145 ,66 2211 ,67 2278 ,68 2346 ,69 2415 ,70 2485 ,71 2556 ,72 2628 ,73 2701 ,74 2775 ,75 2850 ,76 2926 ,77 3003 ,78 3081 ,79 3160 ,80 3240 ,81 3321 ,82 3403 ,83 3486 ,84 3570 ,85 3655 ,86 3741 ,87 3828 ,88 3916 ,89 4005 ,90 4095 ,91 4186 ,92 4278 ,93 4371 ,94 4465 ,95 4560 ,96 4656 ,97 4753 ,98 4851 ,99 4950 ,100 5050 ,

代数式の計算¶

素因数分解

show(factor(720))    # この場合.show()を付けるとエラーになる。

1変数多項式の因数分解

X1=(x+x^2-2*x)*(3*x^3-3)   # 多項式をXに代入する。
X1.show()
X2=factor(X1)
X2.show()

展開

expand(X2).show()

Pythonプログラムの中からこういった函数を使えます。というか大雑把に言えば、実は文法的にはPythonの枠組みに基づいて、さらに数学の式を記述・計算できるようにしたものがSageだと言えます。

for i in range(9,25):
    factor(x^2+10*x+i).show()

記号微積分¶

f(x)=sin(x)  # 1変数函数fの定義
f.show()

$x\mapsto\text{式}$ は引数$x$を与えて右側の式の値を返す函数を表します。

diff(f,x).show()    # 記号微分

g(x,y)=sin(x)*cos(y)    # 2引数函数の定義
g.show()

diff(g,x).show()    # 偏微分

integral(f,x).show()    # 不定積分

有理函数の不定積分の例です。手計算するとかなり面倒です。

h(x)=1/(1+1*x^2+x^4)^2
h.show()
integral(h,x).show()

逆三角函数が結果となる例です。

f1(x)=sqrt(1-x^2)
f1.show()
show(integral(f1,x,hold=true)(x),' =',integral(f1,x)(x))   # 不定積分
integral(f1,x,hold=true).simplify_full().show()

同じ函数の定積分の例です。

Y=integral(f1,x,0,1)
Y.show()

ガウス函数(正規分布の密度函数)の定積分の例です。

nd(x)=1/sqrt(2*pi)*e^(-1/2*x^2 )   # σ=1のガウス函数
nd.show()
integral(nd,x,-oo,oo)    # -∞から∞までの定積分

1

定数値を変えていって不定積分するプログラムの例です。

for i in range(1,5):
    show(integral(1/(x^2+i*x+1),x,hold=true),' = ',integral(1/(x^2+i*x+1),x))

色々な計算¶

次でassumeというのは変数の型や範囲を仮定するためのものです。こうした仮定をすることでSageによる式の変形をやりやすくしています。

var('n m')
assume(m,n,"integer")    # mとnは整数型だと仮定
assume(m>=0,n>0)         # mは非負、nは正だと仮定
X=product(n,n,1,m,hold=true)
Y=product(n,n,1,m)
show(X,' =',Y)
var('y')
X=sum(x*sin(x),x,0,y,hold=true)
show(X,' =',X.simplify_full().simplify_full())   # 何回もsimplifyしないといけない場合がある
assumptions()    # 仮定を表示(このセル以外の仮定も表示される)

[m is integer, n is integer, m >= 0, n > 0]

var('i m')
assume(i,m,'integer')    # iとmは整数だと仮定
assume(m>=0)             # mは非負だと仮定(これらは必ずしも必要ないかもしれない)
f2(x,m)=sum(x*sin(i*x),i,0,m-1,hold=true)    # この記法は将来的には無効になる
show(f2(x,m),' =',f2.simplify_full())
diff(f2.simplify_full(),x).simplify_full().show()
assumptions()

[m is integer, n is integer, m >= 0, n > 0, i is integer]

線形代数¶

A=matrix([[1,2],[3,4]])
x=vector([1,2])
y=matrix([[1],[2]])
show(A)
show(x)
show(y)                 # ベクトルと1x2マトリクスの表示の違いに注意
show(A*x)
show(x*A)
show(A*y)               # 縦ベクトルはマトリクスの一種
show(transpose(y)*A)    # 転置しないとエラーとなる。

B=matrix([[1,1],[2,2]])
show(B)
show(A-B)    # 行列の引き算。和+、積*も可能。

show(A^-1)    # Aの逆行列。除算/によっても求められる。

det(A)  # Aの行列式

-2

特性多項式、固有値のリスト、固有値と固有ベクトルのペアのリスト。

show(A.charpoly())
show(A.eigenvalues())
show(A.eigenvectors_left())    # 重複度も求める

2次元グラフ¶

以下はガウス函数(正規分布の密度函数)の定数倍のグラフの例です。グラフを描く場合にはxを記号変数として宣言しておく必要があります。

var('x')    # xを記号変数として宣言
plot(e^(-x^2),x,(-3,3)) + plot(e^(-(x+1)^2/2)/2,x,(-3,3),color="red") # 2つのグラフを表示

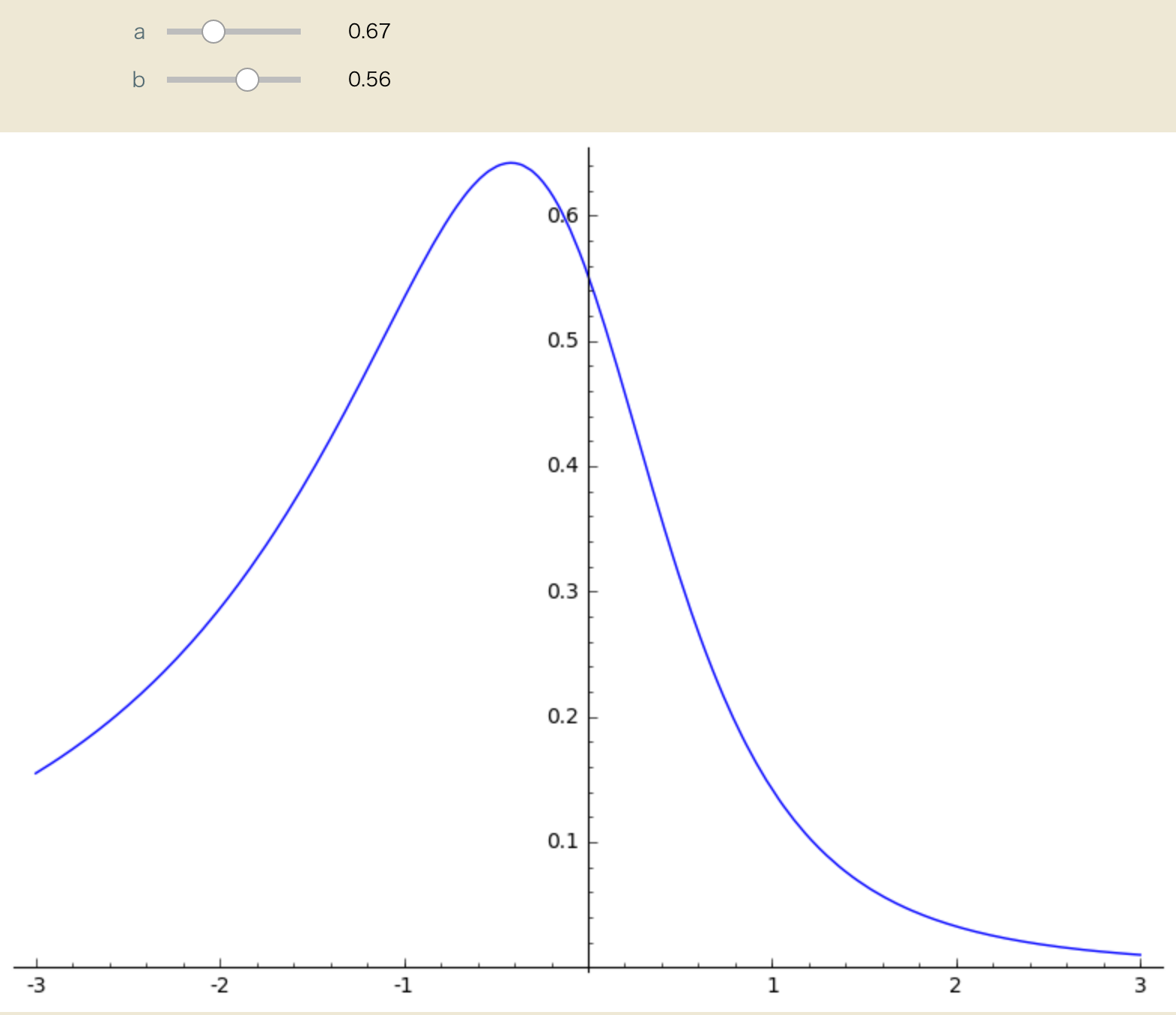
次はパラメータをインタラクティブに変更できるグラフの例です。ジョンソンSU分布システム(説明略)を例にとっています。 erfというのはガウス函数の不定積分(の一つ)です。

@interact
def _(a=slider(0,2, step_size=0.01),b=slider(-3,3, step_size=0.01)):
    show(plot(diff(erf(a*arcsinh(x)+b),x),x,(-3,3)))

3次元グラフ¶

次の例は2次元正規分布の密度函数(の定数倍)を3次元グラフ表示する例です。マウス操作により拡大・縮小、上下・左右の回転、移動を行えます。

var('y c')
assume(c>0)
f2(x,y,c)=exp(-(x^2+x*y+y^2))
show(f2)
plot3d(f2(x,y,1),(x,-3,3),(y,-3,3))

陰関数による楕円体表示の例。 implicit_plot3dの最初の引数の式=0の解集合を描画します。

var('y, z')
implicit_plot3d(2*x^2 + y^2 + 1/2*z^2 - 1, (x,-1.5, 1.5), (y,-1.5, 1.5), (z,-1.5, 1.5))

例:$n$次正方行列から成る有限モノイドの生成¶

この例は、$n$次正方行列のリスト(生成系)を指定して、それらから行列の積により生成されるモノイドを集合として求めるようなプログラムとして書かれたものです。生成したいのが群の場合で積により生成されない生成系の逆元がある場合、それらを生成系に加えておく必要があります。

説明していないPythonの言語要素や機能を使っています。もし知らない概念が出てきてそれでも内容を知りたければネット等で調べながら読んでください。

import itertools           # itertools.productを利用するため。

# get the monoid generated by l.   群の場合で逆元が生成されないならそれらを加えておくこと
def generate_monoid(l0):                # l0: a list of n x n matrices
    l0=[copy(x) for x in l0]            # 行列リスト(生成系)lをコピー
    map(lambda x:x.set_immutable(),l0)  # ディクショナリのキーとして使うためimmutableにする
    E=identity_matrix(l0[0].nrows())    # 単位行列生成
    E.set_immutable()
    n = 1        # nは生成された元の個数
    show(n,':',E)
    l = {}       # 生成された元のディクショナリ
    l1 = {}      # 新しく生成されlに追加される元のディクショナリ(hashテーブル)
    l1[E]=n
    m = 0        # これまでにm回生成系の積を取った
    while(list(l1.keys()) != []):    # 新しく生成された元がなければ終了
        m = m + 1
        print(m)                     # 積の回数を参考のため出力する
        l.update(l1)                 # l1の元をlに追加する
        t = itertools.product(l1,l0) # l1 x l0の積集合をtに代入する
        l1 = {}                      # l1は新たに生成された元のディクショナリ
        for x,y in t:                # l1 x l0の各対について
            for r in x*y, y*x:       # 実際に積を求める。非可換なので2回計算するのをループとした
                r.set_immutable()
                if not r in l and not r in l1: # rがlの元でもl1の元でもない時
                    n = n + 1        # 新しい元のカウントアップ
                    show(n,':',r)
                    l1[r]=n          # rをl1に付け加える
    return l                         # 返り値は生成された元をキーとするディクショナリ

# setup the group generated by S and H in l.
l=[matrix([[-I+1,0],[0,I+1]])/sqrt(2),matrix([[0,I],[I,0]])]
show(l)
show(generate_monoid(l))

1

2

3

4

5

6

Table of Contents