Table of Contents¶
R+Jupyterによるプログラミング ほんの入り口¶
ここではJupyter Notebookでプログラミング言語R(R入門)を用いて演習を行います。少ない時間でプログラムとは何であるかを原理的に理解することと、文房具としてのプログラミングをある程度マスターすることを目的としています。本格的なプログラミングを学ぶためにはそれぞれのプログラミング言語の演習を履修することをお勧めします。
Jupyter Notebookとはプログラムとその実行結果(値(文字列含む)、グラフ、表形式)、文章(説明)を混在させて編集・表示を行えるツールです。Jupyterのデータの処理を行うプログラムはサーバ方式で動作し、それにwebブラウザから接続して使います(OSのメニュー等からJupyter Notebookを起動すれば自動的にブラウザが立ち上がってローカルに動作するJupyerのサーバに自動的に接続します)。メディアセンタのWindowsにはRの処理系がインストールされています。但しJupyter Notebookの中から使うようにはインストールされていません。従ってメディアセンタのPCを使ってこの資料に従って演習を行う場合、Jupyterを利用せずに演習を行うことになります。
一方Rの処理系とJupyter Notebookはフリーソフトウェアであり、BYODのPCに無料でインストール可能です。この場合には両方をペアにして演習を行うことが可能です。
R+Jupyterのインストール方法¶
Rの処理系がインストールされていない場合、インストールしないとR言語のプログラムを実行できません。当然ながらインストールは一回行えばよいです。またRの処理系をインストールする場合、この資料ではJupyterも同時に利用できるようにインストールすることを推奨します。そのためにはAnacondaというソフトウェアをインストールし、その後そのソフトウェアの機能を利用してR-Studioをインストールします。
Anacondaのインストール方法についてはJupyterの資料を参照してください。
3者共通の追加の作業¶
Anacondaがインストール済みであれば、Anaconda-Navigatorというコマンド/アプリケーションを起動し、 R-StudioのインストールボタンをクリックすればR言語の処理系がインストールされ、 R-Studioが使えるようになると共にJupyter NotebookからRの処理系(kernel)を使えるようになります。 手許のPCでUSB3接続の外部SSDにインストールした場合に試したところ、約15-20分ほどかかりました。
Anaconda-Navigatorの起動方法はOSによって異なります。 Windowsの場合にはメニューからかコマンドプロンプト/Powershellから起動します。 MacOS Xの場合はアプリケーションフォルダのアイコンをクリックして起動するか仮想端末から起動します。 Linuxの場合にはメニューあるいは仮想端末から起動します。 いずれの場合にもAnacondaのインストール時の権限が必要となる場合があります。
既にRの処理系がインストールされていた場合¶
Anacondaとは別に、R-Studioを過去にインストールしていた場合など、既にPCにRの処理系がインストールされて正常に動作している時に、AnacondaでR-StuidoをインストールするとRの処理系が結果的に2重にインストールされます。 この場合、保証するわけにはいきませんが、新しくインストールされるR-StudioはAnacondaのインストール先のディレクトリに追加でインストールされるため、問題ない場合が多いようです。 但し記憶領域が無駄になりますし、 同じ言語の環境が2つあることに積極的な意義を見出せない場合にはあまり意味はないと考えられます。
Jupiter Notebookの起動と終了・利用方法¶
この段落で説明する起動方法は別ページでの説明とほぼ同じです。Anaconda-navigatorでR-Studioを追加インストールした場合にはこの段落の方法を取ることになります。
JupyterからRを使うように起動する方法はいくつかありますが、ここではメニューによる方法を紹介します。 まずメニューから選択するなどしてJupyter notebookを起動します。 するとwebブラウザが起動してJupyterの表示が出ます。以降はJupyturサーバを停止する前まで、webブラウザでJupyter Notebookを利用することになります。
Jupyter Notebookの利用方法については別ページを参照してください。但し、この資料のプログラムを動かすには、新しいnotebookを作るときのメニューでkernelをRとするか、あるいは後で[kernel]メニューから[Change Kernel]→[R]を選ぶ必要があります。これらのメニューにRの項目が表示されない場合、Rのkernelが正しくインストールされていない可能性があります。Notebookの右上にRの言語名が表示されていることを確認してください。
Jupyterを終了するには別ページに従って全てのnotebookを閉じてから、Jupyterのコンソールで例えば[ctrl]+cを入力して停止するか訊いてくる場合にはyを入力します。するとJupyterのサーバが停止します。
[ctrl]+c等が効かなければ最初からコンソールウィンドウを消すことになります。
学習方法¶
このページを表示しながら、プログラムのコード部分(In [ ]:の右側枠内の部分)を順にJupyterのセル(やはり枠内の部分。プログラムなのでCode属性にする)に手入力するかコピー&ペーストし、実行します。或いは授業中に提示する予定の、notebookのデータファイルをuploadすることで、直接実行することが可能になります。但し提出課題の部分は自分で入力するなり変更するなりする必要があります。
Jupyter notebookでR kernelが正しく動作しない場合には、他の方法でRのプログラムを動作させる必要があります。 例えばR-Studioを起動し、そこにプログラムをキーボードから打ち込むか、コピー&ペーストして実行します。 ただしこの場合には下記のプログラムのうちの一部がそのままでは動作しない可能性があります。 特にグラフィクス関係のプログラムがそうでしょう。
課題の提出方法¶
課題の回答を作成して動作確認したらコピー&ペーストによりプレーンテキストのファイルとして提出してください(次回以降も同様)。
ファイル名: 課題提出用ID-課題番号.r
ファイル名の例: e20000-kadai07.r
右側の課題番号は毎回変わりますし、左側の課題提出用IDは各自異なります。
注意点:¶
- 適宜コメントを記述してください。
- プログラムについては、提出前に動作することを必ず確認してください。
- ファイル冒頭にもコメントとして課題提出用IDと課題番号を記してください。
- ファイル中に、第三者が個人を特定できる情報を書かないでください。
- ファイル名はすべて半角としてください。
- 上記注意点が守られていない場合、評価対象とならない場合があります。
最初のプログラム¶
下の「1+2」はこれで一つのプログラムです。これを実行する(評価する)にはマウスでクリックして下のセルを選択し、(存在する場合は)ウィンドウ上方の[>|]のボタンをクリックするか、SHIFT+returnキーを押します。Out[..]: 3というように値3が表示されれば正常に動作しています。
1+3
次のセル中に加減乗除(+-*/)による数式を書き、同様に実行してみてください。セルの中を書き直して再実行できます。
10+4*(3/4+100)+1011
これはR(R入門)というプログラミング言語のプログラムとして対話的に実行しています。一応ウィンドウ右上にRなどと表示されていることを確認してください。プログラムの実行の仕方としてバッチ式と対話式という方式があり、前者は(複数の時もありますが)一つの定まったプログラムにデータを与えて処理を行う方式です。後者はプログラムの処理系にプログラムの断片を入力しつつ、対話的に小さいプログラムの実行と結果の表示を繰り返し行う方式です。
対話的に実行する方がとっつきやすいので、この資料では対話的に実行する方法で解説を行います。ただし、Jupyterの場合セルごとに実行を行うため、実行の順序によって処理系(プログラムの実行を行うプログラム達。本体部分はかなりの部分が機械語でできていたりします。実行する対象のプログラムはR等の、人間が理解しやすい高級言語で書かれたものです。大きく分けてコンパイラ方式とインタプリタ方式があります)の状態が異なる場合があります。また、そもそも実行していないセルがあると、その内容に依存する他のプログラムの断片がうまく動作しない場合がありえますので注意が必要です。これについては後で説明します。
ここでRのversionを確認しておきます。以下ではversionの値を求めています。
version # #から右側はコメントとなる
R言語のチュートリアル等を参照する際にはversionが近いものを参照してください。
変数¶
変数はほとんどのプログラミング言語において重要な概念です。変数(variable)とは、何らかのデータを格納する箱だと思ってください。箱には名前があり、それを変数名と言います。後で出てくるように違う箱だが同じ名前が与えられる場合があり、その場合についての理解が必要です。Rの変数名は、ASCIIの範囲では英数字とピリオド「.」、アンダースコア「_」の列です。日本語の文字も使えます。R - Variables等を参照してください。
また、Rを含めて手続き型のプログラミング言語ではプログラムの実行途中で値を変更することができる種類の
変数があり、それが計算の状態変化を表します。このようにプログラムの実行途中で値の変化が可能な変数をmutableな変数と言います。変数の箱に値を入れることを代入(assignment)と言い、Rの場合には<-や<<-を使って表します。
変数には種類があり、どのような種類の変数が使えるかはプログラミング言語により変わります。しかしまずここではそれらのうち大域変数(global variable)という、プログラム(ファイル内)のどこからも参照できる(例外があります)変数のみが出てきます。大域変数についてはそれらの箱はプログラムの実行開始時(あるいはその変数が存在することがわかった最初の時点)からプログラムの実行終了時まで存在し続けます。
以下、上から順番に各セルを実行してみてください。例えばx<-式、で式の値を計算し、結果をxに代入します。Rでは代入文がそのままでは値を持たないため、変数をその後に記してその値を参照するか、()で囲んで値を得る必要があります。なお#から右側はコメントとして扱われ、この部分は実行されません。
(x<-11) # 変数xに11を**代入**する。()で囲んで値を得ている。
(y<-23)
(z<-x*y)
x
z*z
(x<-12)
(z<-x*y)
(z<-x+3) # z に3を加える
(z<-2*z) # zの値を2倍する
この例のように、変数には値を格納することが出来ます。その後の命令の列が全く同じでも、変数の値によって計算は変わってきます。上から順に実行した場合には最初xの値が11であり、それに依存して決まるzの値は最初253になります。しかしその後xの値が12に変更されてからz<-x*yという同じ命令によってzの値は276という異なる値になります。変数は電卓のメモリと同じ用途で用いることが可能です。
上から順に実行した場合、最初のz<-x*yでzの値は253になりますが、その後下の方の命令を実行してxの値が異なる値に変化してから(下の方のではなく)最初と同じセルのz<-x*yを実行すると、zの値は異なるものとなります。また、x<-11やx<-12を実行する前にz<-x*yを実行するとxの値が定義されていないためにエラーになります。このようにセルの実行順序によってエラーが起きたり変数の値を含めて状態が変化することに注意してください。また、z<-z+3のように実行の度にzが増加するため実行回数が影響を与える場合もあります。上から順に実行すれば実行回数に関わらず正しく動くようなnotebookとするのが望ましい場合が多いです。
Rでは数値以外にも様々なデータを扱います。例えばデータの列である配列や文字列などがあります。データの種類のことを一般にデータ型といいます。プログラムの実行前に式が表すデータの型が定まるようなプログラミング言語を静的型付けの言語と言います。それに対し、データ型が実行前に決まらず、実行時にチェックされる言語を動的型付けの言語と言います。Rは動的型付けの言語に分類されます。
静的型付けの言語はプログラムの実行前に、ある種のプログラムのミス(BUG)がないことを自動的にチェックできます。特に強い型付けという種類に分類される言語では、実行前のチェックを通っていればデータ型に関するエラーが実行時に起きないことが保証されます。ただしプログラミングを学ぶ際にデータ型に関する理論をある程度学ぶ必要がありますし、十分広い枠ではありますが、一定の枠に嵌ったプログラムのみを書けることになります。動的型付けの言語ではデータ型のエラーの実行前のチェックは行われず、実行時に検出されることになります。
なお、Rでは以下のように代入文を書くことも可能です。
x <- 10+2
2*3 -> y # 右側の変数への代入。
z = 2+3 # = による代入。
assign("t",5*6,-1) # 指定した文字列の変数名を持つ変数への代入。環境を指定したり様々なことができる。
c(x,y,z,t) # この場合cは後述のベクトルを作る。ここではいくつかの値を並べて出力するために使っている。
条件判断¶
ここまではほとんど電卓と同じように計算を行ってきただけでした。しかし今から出てくる条件判断と繰り返しは、通常の電卓にはないものであり、計算機を有用な道具とするには必須のものです。Rの条件文は以下のような構文になります。改行やインデント(字下げ)はR処理系にとってそれほど意味はなく、主に人間にとっての読みやすさのためにあります。但し以下で例えば式1と2を同じ行に記述する場合には間に「;」(セミコロン)が必要です。
構文:
if (条件式) {
文1 # 条件がTRUEであればelseまでの部分のみが実行される。
文2 # 改行は空白と同じく区切りである。
.
.
} else { # elseから後の}まではなくてもよい。
文a # 条件がFALSEであればこの部分のみが実行される。
文b
.
.
}通常、条件式の部分には等しいかどうか(==,!=)大小関係等(<,>,<=,>=)やそれらの組み合わせ(&&,||,!で組み合わせる)等、真偽値をとるような式を記述します。なおelse {から対応する}の前までの行はなくても構いません。その場合は条件式がFALSEであった場合、条件文内では追加で何も実行されません。
次の具体例では条件部分の真偽により式の値が変化します。==は両辺が等しい時TRUE、等しくない時FALSEとなります。Rではif文そのものが値を持つ場合があることがわかります。
if (1==1) 1 else 2
この例のように、文が一つしかない場合には{}を省略して同じ行に書けます。次の例も同じです。
(if (1 == 1) x<-1 else x<-2)
但し単にelseの前で改行するとエラーとなります。
if (1 == 1) x<-1
else x<-2
範囲がはっきりするように{}や()で囲めば問題ありません。
{if (1 == 1) x<-1
else x<-2}
(if (1 == 1)
x<-1
else x<-2)
Rではインデントの量は特に意味はありません。従って同じプログラムを下のように記述できます。
(
if (1 == 1)
x<-1
else
x<-2
)
c(1==1, 1==0, 1!=0, 1>2, TRUE || FALSE, TRUE && TRUE, !TRUE) # ベクトルとなる
繰り返し¶
Rで繰り返し処理を記述する方法は多数あります。ここではそれらのうちの一つ、forによるものを紹介します。
構文:
for (変数 in ベクトル) {
文1 # 変数の値をベクトルの各要素に変えて}までの文が繰り返し実行される。
文2
.
.
}ベクトルというのはRの基本的なデータ型であり、
数値など同じ種類の基本的なデータが直線状に並んだものです。
例えばn:mとするとnからmまでの整数を並べたベクトルとなります。
3:9
for (i in 1:100) { # 1:100は1から100まで並んだベクトル。
cat(i) # catは引数(ひきすう、argument)の値を改行なしで出力する。
cat(",")
}
for (i in 1:-1) { # 1:-1は1から-1までを意味する。iが各ステップで減ってゆく。
cat(i,"")
}
なおif文やfor文は入れ籠にすることができます。
函数定義と、変数のスコープ¶
新しい函数を定義することが可能です。例えば二次方程式$ax^2+2bx+c=0$の解(の一つ)を求める函数quadraticは以下のように定義できます。
quadratic <- function(a,b,c) { # a,b,cは変数であり、これらを仮引数(かりひきすう)と呼ぶ。
return (-b + sqrt(b^2 - a*c))/a # 返り値。a^b はaのb乗
}
quadratic(1,3,1) # 1,3,1を実引数(じつひきすう)、この文自体を函数呼び出しと言う。
Rにおける函数の定義は、函数を変数quadraticに代入しているように見えます。
実際、変数quadraticを見てみると函数が入っています。
quadratic
また、函数本体部分を実引数に適用しても、上のquadratic(1,3,1)と同じ結果が得られます。
(function(a,b,c) {return (-b + sqrt(b^2 - a*c))/a})(1,3,1)
(function(...)...)の括弧内の部分を一般に無名函数(あるいはλ式)と呼びます。
函数定義を行う際に名前をつけるのが基本で、λ式があっても(一見)別概念と取ることも可能な言語が多い中、
Rでは各函数定義に無名函数が出てくるようになっています。
局所変数と大域変数¶
変数には局所変数と大域変数があります。 局所変数はある範囲内のみで有効で、たいていの場合実行途中で一時的にしか存在しない変数です。 次の例を見てください。
test1 <- function() { # 引数が一つもない函数。
newvariable_fun <- 1 # 函数定義の中の場合、代入先の変数は局所変数となり、定義の中だけで有効である。
}
test1()
newvariable_fun # 未定義なのでエラーとなる。
変数の有効範囲のことをスコープといいます。 この例でnewvariable_funという変数のスコープは函数test1の定義内であり、 この変数は局所変数です。 大域変数の例は変数の項目を参照してください。
局所変数と同じ名前の大域変数がある場合、それらは函数内部からは基本的に参照できなくなります。大域変数と局所変数で同じ名前の変数がある場合、あるいは函数呼び出しが何重にも重なった場合に同じ変数名の変数が出てくる場合があります。それらは変数名が同じなだけで、「箱」としては別物であることに注意してください。
函数定義中の変数¶
まず、函数定義の中の変数は仮引数を含めて基本的にスコープをその函数定義内とする局所変数となります。 但し通常次のような例外があります。
- 函数定義内で
<<-による代入先の変数(->>も使える)。 - 函数定義内で
<-により代入先となるまでの変数。ただし仮引数は除く。
前者については、<<-の左側が函数定義内の局所変数達のスコープに含まれない、ということもできます。
大域変数の最初の説明で、大域変数への代入なのに<-を用いていたのは、函数定義の中ではないからです。
後者の場合、<-による代入が起きるとその時点で局所変数の箱が作られます。
従ってRの場合、スコープが完全にレキシカルかというとそういうわけではないと言えます。
例えば条件文やループと組み合わせると、同じ変数名への参照が場合によって大域変数だったり局所変数だったりすることがあり得るからです。
ですがたいていの場合、レキシカルスコープと考えてよい動作をすると考えられます。
また後者の変数は大域変数になるとは限らず、
外側のスコープの局所変数かもしれません。
x <- 0
y <- 1
z <- 2
t <- 3
test2 <- function() {
t <- 4 # このtはtest2の定義中で有効な局所変数。つまりtのスコープはtest2の定義の範囲。
test3 <- function() { # このように函数定義を入れ籠にすることもできる。
t # test3の実行時にtへの代入は行われない。故にこのtは一つ外側のtと同じで値はtest3が呼び出された時のtの値4。
}
cat("x =",x,"\n") # このxは函数定義の外側のxで値は0。
x <- 3 # 函数定義の中で代入先になっているためxは別の箱となり、局所変数となる。外側のxの値は変化しない。
cat("x =",x,"\n")
y <- 4 # yは局所変数。
y <<- 5 # 外側の大域変数yに代入するには<<-を使う。->>も使える。局所変数のyの値は変化しない。
cat("y =",y)
c(z,test3()) # zには代入せず参照するだけなので函数定義の外側から継承されて大域変数となる。
}
test2()
c(x,y,z) # 函数定義の外側のxは函数定義中のxと同じ変数名だが別の箱。
y <- 0
test3 <- function(x) {
if (x == 0) y <- 1 # この代入が起きるとyが局所変数となる。
y # x == 0の時はこのyは局所変数。y != 0の時はこのyは大域変数。
}
test3(0)
y
test3(1)
y
ループ中の変数・条件文中の変数¶
函数定義の場合とは異なり、forのようなループの場合やif文ではスコープが別になりません。
例題: フィボナッチ函数と階乗¶
ここまでの知識で定義できる函数の例題を見てみます。
フィボナッチ函数とはfib(0)=1, fib(1)=1, fib(n)=fib(n-2)+fib(n-1)として再帰的に定義される函数です。自然界のいろいろなところで現れることが知られています。
fib <- function(i) {
x <- 1; y <- 0
for (i in 0:i) { # Rではfor (i in (x:y))が、x>yでもループを実行することに注意。
y <- x + y
x <- y - x
}
x
}
c(fib(0),fib(1),fib(2),fib(3),fib(4),fib(5),fib(6)) # この式は値の組みを結果とする
fact <- function(i) { # 階乗を計算する函数
y <- 1
if (i > 0) for (i in 1:i) y <- i*y
y
}
list(fact(0),fact(1),fact(2),fact(3),fact(4),fact(5),fact(6)) # この式はリストを結果とする。
大きい値の場合には無限大を意味するInfが結果となります。
fact(300)
グラフ¶
ここでグラフを描く方法を書いておきます。レポートを作成する際などに大変便利な機能であり、定規や色鉛筆などを超える文房具としてプログラムを利用することになります。ただしこの資料の今の進度よりは相対的に難しい概念が出てくる部分があります。
ここではJupyter Notebookにインライン(同じ文章中)で表示します。
r <- 0:14 # 0,1,2,3,...,14というベクトル
plot(r,mapply(fib,r)) # ベクトルの各値にfibを適用したベクトルを作り、それらにより点をプロットする。
# mapplyにより函数fibを適用し、r中の各値の結果のベクトルを作る。
0,14を他の値に変えれば範囲が変わり、fibを他の函数に変えれば表示する函数が変わります。函数定義を他で行なってそれを実行し(読み込ませ)てから変更した上のプログラムを実行すればグラフが書き換わります。
ここでmapply(fib,r)はベクトルrの各値に対し函数fibを適用した結果のベクトルを作ります。plotは2つの列を引数とし、それらを座標として点を平面にプロットします。
次の例はもう少し実用に近い例であり、どのように指定すれば表示がどうなるのかわかると思います。
x = 0:14
fibl <- mapply(fib,x + 1)
factl <- mapply(fact,x)
value <- cbind(fibl,factl)
matplot(x,value,type="b",log="y", pch=c(15,0), lwd=3, lty=1) # この場合ラベルは変数名となる。
# y軸はlogスケール
legend("topleft", legend=c("fib(x)", "fact(x)"), pch=c(15,0), lwd=2, lty=1, col=c("black", "red")) # 凡例
title("fibonatti and factorial") # タイトル
表¶
グラフではなく表形式で表示してみます。 これはDataFrameをそのまま出力しているだけです。
#using DataFrames # このセルは函数定義のセル達の後に実行する
data.frame(x=0:14,fib=mapply(fib,0:14),fact=mapply(fact,0:14))
キーワードの補完¶
Jupyterに限らず、ある種のキーワードを補完する機能がついている場合があります。Jupyterの場合には[TAB]キーにより補完を行います。
これはR以外のkernelの場合にも大抵使える機能です。
Codeセルでキーワードを途中まで打ち込んで[TAB]キーを押すとそれを先頭とするキーワード候補の選択メニューが表示され、選択できる状態になります。
# 次の行に例えば「r」を入力し、`[TAB]`キーを押すとrで始まるキーワード達の選択メニューが表示される。
r
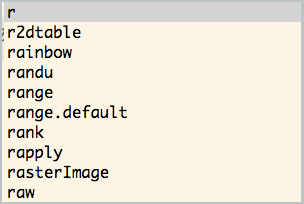
候補が多数ある場合にはスクロールして選択します。
逆にもしも候補が一つもない場合には何も表示されません。
一つしかない場合にはその候補の残りの文字列が自動入力されます。
この機能を指して補完(completion)と呼びます。
長いキーワードを入力する場合に一意的になるまでキー入力後、
[TAB]により補完するとキーストローク数が減り、
誤りも減らせます。
函数・変数等の説明¶
R kernelの場合、Codeセルの最初に「?」を入力してその後函数名を入力し、
[SHIFT]+↩︎を押すと、それについての説明が表示されます。
これはRの場合に使える機能ですが、他の言語の場合にも類似の機能が使える場合があります。
?print # ブラウザのウィンドウ下部にprintの説明が表示される。
??concatenate # ドキュメントから文字列を検索する。やはり下部に表示。
最初の課題¶
ここまでに学習した事柄を使って、引数として与えた2つの整数の間のすべての整数の和を求める函数sum2をRで記述してコピー&ペーストしてメールにて提出せよ。ただし2つの整数のうちの小さい方は含め、大きい方は除くこと。2つの整数が等しい場合は0である。数値演算は和と差のみしか使ってはならない。課題の提出先は従来と同じ、課題提出用ID-kadai07.rというファイル名とすること。
# e80123 kadai07 課題提出用IDを書き換え
#
sum2 <- function(x,y) {
if (x == y) return(0)
if (x > y) {x <- x + y; y <- x - y; x <- x - y}
y <- y - 1
for (x in x:(y - 1)) y <- y + x
y
# x+y # 正しいプログラムに書き換えること
}
c(sum1(-2,1), sum1(1,-3), sum1(10,13), sum1(-100,1))
# -3 -6 33 -5050
再帰呼び出し¶
これまでに、フィボナッチ数列や階乗計算のプログラムを例題として示して解説しました。それらは元々再帰的に定義されています。プログラミング言語によっては再帰的に定義された数列等を再帰的なプログラムで表現できる機能を備えています。Rにもその機能はあり、例えば次のようにしてフィボナッチ数列や階乗計算を行うプログラムを記述することができます。
fib_r <- function(x) {
if (x == 0) 0
else if (x == 1) 1 # if文の最初の条件を満たさない時にelseifの条件がチェックされる
else fib_r(x - 1) + fib_r(x - 2) # 再帰呼び出し。
}
c(fib_r(0), fib_r(1), fib_r(2), fib_r(3), fib_r(4), fib_r(5))
fact_r <- function(x) {
if (x == 0) 1
else x*fact_r(x - 1) # 再帰呼び出し。
}
c(fact_r(0), fact_r(1), fact_r(2), fact_r(3), fact_r(4), fact_r(5))
このように、fib_rやfact_r自身の定義の中でまたそれらを呼び出すことを一般に再帰呼び出し(retursive call)と呼びます。これもプログラミングにおける重要な概念の一つです。前に例題とした再帰呼び出しによらないプログラムと比較してみてください。ただしfibについては、再帰呼び出しのfib_rの方は非常に効率の悪いものとなっています(なぜでしょうか)が、同じ再帰呼び出しでも効率の良いプログラムを書くことも可能であることを申し添えておきます。
再帰呼び出しのプログラムを書くときの考え方¶
Rのような手続き型の言語(ここでは変数への代入文があり、計算状態を変化させる操作の列、即ち手続きとしてプログラムを記述する種類のプログラミング言語を手続き型としています。もちろんRで函数的にプログラムを書いてゆくことも可能でしょう)の場合には、再帰呼び出しのプログラムを書く際に、一般には「再帰呼び出しを行う」という操作を行うことと、その時の状態を意識する場合が多いかもしれません。しかしこれまでに出てきたようなフィボナッチ函数や階乗のような、いつ計算しても値は同じだし、計算の状態の変化を引き起こさない場合(つまり値を返す以外の状態の変化である副作用(side effect)がない場合)、即ち函数定義としてプログラムを与えている場合には、再帰的プログラムを書く時に宣言的に考えることが可能です。またこのように考えた方がプログラミングを学びたての場合には理解しやすい人もいますし、すでに手続き的な考え方に慣れている人にとってはある意味新鮮な別の考え方であると思います。再帰呼び出しを行う函数を定義するときの考え方を以下に記述します。
- 最も基本的な引数の値の場合には、再帰呼び出しによって値を与えないようにする。
- 再帰呼び出しについては、呼び出された函数が正しい値を持つと仮定してよい。
- 再帰呼び出しの引数が、元の引数よりある意味簡単なものになっている必要がある。
- 再帰呼び出しのある函数は未定義の(手続き的に考えた場合には停止しない)場合がある。
1.はfib_rについてはfib_r(0),fib_r(1)の場合、fact_rについてはfact_r(0)の場合が該当します。2.はfib_r(x - 1)やfib_r(x - 2)、fact_r(x - 1)が正しい値を返すとしてプログラムを書いています。3.はこれらの場合、値が少ないフィボナッチ数や階乗の値を計算する方が、元のフィボナッチ数や階乗の値を計算するよりも簡単だと考えられます。4.について、2つの函数は負の数に対しては計算が止まりません。4があるため、正確には定義しているのは函数ではなく部分函数(partial function)であるということになります。
考え方の内3が一番曖昧で、どのような意味で簡単な引数で再帰呼び出しをするかは場合によって異なります。但し大抵の場合は直観的にわかる範囲の場合が殆どです。あらゆる場合に適用できるような、この部分の厳密な定式化はある意味不可能であることがわかっています。
但し以上の考え方は、あくまで副作用のない場合であり、次に出てくるタートルグラフィクスの再帰的な描画の手続きの場合、基本的にはやはり手続き的な考え方をすることになります。 手続き的に考える場合、仮引数などの局所変数は呼び出しごとに別物となります。
タートルグラフィクス¶
画面に図形を表示する演習を行うと興味を引かれる人が多いようであるという理由で、ここではタートルグラフィクスによる演習を行います。タートルグラフィクスとは、タートル(亀)の動きによりさまざまな図形を描くというグラフィクスの一方式です。いわゆるフラクタル図形等の描画を簡単に行うことができます。タートルグラフィクスは、それ自身を扱うのが容易で、しかもタートルグラフィクスの基本プログラムを記述するのも簡単なため、入門的なコースや説明でよく使われるものの一つです。
タートルグラフィクスは次のセルで定義したものを使います。 タートルをRのようなオブジェクト指向プログラミングを行える言語で実現する場合、タートルをオブジェクトとし、マルチタートルグラフィクスとするのが自然です。以下ではそのように記述しています。
turtle_class <- setRefClass (
Class = "Turtle",
fields = list(
x = "numeric",
y = "numeric",
v = "numeric",
pendown = "logical",
theta = "numeric",
col = "character"
),
methods = list(
initialize = function(){x <<- 0.5; y <<- 0.5; v <<- 0.0015;
pendown <<- TRUE; theta <<- 0.0; col <<- "black"},
forward = function(d){
d <- v*d;
x1 <- x + d*sin(pi/180.0*theta); y1 <- y + d*cos(pi/180.0*theta);
if (pendown) segments(x,y,x1,y1,col=col);
x <<- x1; y <<- y1
},
rotate = function(t){theta <<- theta + t},
verocity = function(v1){v <<- v1},
home = function(){x <<- 0.5; y <<- 0.5},
north = function(){theta <<- 0.0},
color = function(c){col <<- c},
up = function(){pendown <<- FALSE},
down = function(){pendown <<- TRUE},
clone = function(){t <- turtle_class$new(); t$x <- x; t$y <- y; t$v <- v;
t$pendown <- pendown; t$theta <- theta; t$col <- col; t}
)
)
但しここでは上のプログラムを読み込ませる必要はありますが、 中身についてはブラックボックスとし、説明を省略します。 興味のある人は調べながら読んでみてください。
Koch曲線、Hilbert曲線、Sierpinski曲線¶
タートルグラフィクスによっていわゆるフラクタル曲線を簡単に描くことが可能になります。なお、グラフィクスのプログラムは環境によって挙動が変化する場合があります。ここでは描画中の画像を見ることができず、結果をinlineで資料中にはめ込んだ形で見られる環境を想定しています。
koch <- function(t, x){ # returnがないのは函数ではなく手続きだから。つまり返り値がなく、副作用(この場合は描画)のみが結果となる。
if (x <= 4)
t$forward(x) # タートルの向きにx進む。ペンが下りていれば描画される。
else {
x <- x/3
koch(t, x) # 再帰呼び出し
t$rotate(-60) # 左に90度向きを変える
koch(t, x)
t$rotate(120) # 右に120度向きを変える
koch(t, x)
t$rotate(-60)
koch(t, x)
}
}
plot.new() # グラフィクスの初期化
t <- turtle_class$new() # タートル生成
t$verocity(0.0018) # 測度の設定
t$rotate(90) # タートルは右向き
t$up() # 描画OFF
t$forward(-300) # 左に移動しておく
t$down() # 描画ON
koch(t,600) # Koch曲線の描画。
hilbert <- function(t,x,y,theta){
if (x >= y) {
x <- x/2;
t$rotate(theta);
hilbert(t,x,y,-theta);
t$forward(y);
t$rotate(-theta);
hilbert(t,x,y,theta);
t$forward(y);
hilbert(t,x,y,theta);
t$rotate(-theta);
t$forward(y);
hilbert(t,x,y,-theta);
t$rotate(theta);
}
}
plot.new()
t <- turtle_class$new() # タートル生成
t$verocity(0.0014) # 速度の設定
t$rotate(225) # タートルは左下向き
t$up() # 描画OFF
t$forward(384*sqrt(2)) # 左下に移動しておく
t$down() # 描画ON
t$north() # 上向き
hilbert(t,384,12,90) # Hilbert曲線の描画。
sierpinski <- function(t,x,y,theta) {
if (x < y) t$forward(x) else {
x <- x/2
t$rotate(-theta)
sierpinski(t,x,y,-theta)
t$rotate(theta)
sierpinski(t,x,y,theta)
t$rotate(theta)
sierpinski(t,x,y,-theta)
t$rotate(-theta)
}
}
plot.new()
t <- turtle_class$new() # タートル生成
t$verocity(0.0014) # 速度の設定
t$rotate(225) # タートルは左下向き
t$up() # 描画OFF
t$forward(384*sqrt(2)) # 左下に移動しておく
t$down() # 描画ON
t$north() # 上向き
t$rotate(90) # タートルは右向き
sierpinski(t,768,6,60) # Sierpinski曲線の描画。
副作用と再帰呼び出し¶
この部分は少々普通ではない説明をしていますので最初は飛ばしてください。課題を解くのにも必要ないと考えられます。
上のプログラムでは再帰呼び出しを行なっていますが、函数には返り値がありません。即ち副作用のみのプログラムです。この資料ではこのような函数を手続き(procedure)と呼ぶことにします。この場合の副作用はウィンドウにタートルの跡を描きつつタートルの位置や向き、色を変更することです。このように副作用のみの場合には再帰呼び出しを行うプログラムの内容の理解やそれを書く場合にどのように考えればよいのでしょうか。これには2つの方法があります。
- プログラムの動作を手続き的に理解し、記述するという標準的な方法。
- プログラムの副作用をタートルへの操作の列であると考え、操作の列全体を結果とする宣言的なプログラムとして捉え直す。
ここでは2番目の理解の仕方を説明してみます。 手続き(函数)が呼び出され、forwardやrotateなどの操作をタートルに行うのを、操作の列として求める函数だと捉えます。それらの操作は順序に意味がありますが、結合律を満たします。即ち$a_i$を個別の操作とすると、$(a_1,a_2),a_3$という操作と$a_1,(a_2,a_3)$という操作は操作として同じことです。また何もしない、という操作も考えられ、それがある種の単位元になっています。こうしてタートルへの操作の列を生成する宣言的なプログラムであると考えることができますが、これだけですと抽象的な説明であって具体性が不十分なので操作の列を生成するような宣言的なプログラムに書き換えてみます。但し$\lambda$式や後で説明するような概念のリストを先走って使っているので、この部分は飛ばしていただいても構いません。またこのような書き換えを行なうと実際に描画が行われる時刻が変わってくるので、その意味では元のプログラムと等価ではなくなります。
次のプログラムでは再帰的に定義されたsierpinskiという函数の代わりにsierpinski_mという副作用のない函数を定義しています。この函数はタートルへの操作の列(配列)を値として返します。但し後で実行できる形式とするために$\lambda$式を使っています。変数への代入が行われていますが、これは一回だけの代入であり、mutableな変数として扱ってはいません。再帰呼び出しの際に同じ変数名の変数に何度も代入が行われますが、これもそれぞれが論理的に別の変数であり、宣言的なプログラムであることに変わりはありません。上のプログラムと見比べてみてください。
但しプログラムの最後のforの部分では、配列中の操作を全て行なって実際の描画を行なっています。この部分だけが手続き的なプログラムとなっています。
t <- turtle_class$new() # タートル生成
sierpinski_m <- function(t,x,y,theta,a0) {
if (x < y) c(a0,function()t$forward(x)) else {
x <- x/2
a1 <- c(a0,function()t$rotate(-theta))
a2 <- sierpinski_m(t,x,y,-theta,a1)
a3 <- c(a2,function()t$rotate(theta))
a4 <- sierpinski_m(t,x,y,theta,a3)
a5 <- c(a4,function()t$rotate(theta))
a6 <- sierpinski_m(t,x,y,-theta,a5)
c(a6,function()t$rotate(-theta))
}
}
a1 <- list(function()t$home())
a2 <- c(a1,function()t$north())
a3 <- c(a2,function()t$verocity(0.0014)) # 速度の設定
a4 <- c(a3,function()t$rotate(225)) # タートルは左下向き
a5 <- c(a4,function()t$up()) # 描画OFF
a6 <- c(a5,function()t$forward(384*sqrt(2))) # 左下に移動しておく
a7 <- c(a6,function()t$down()) # 描画ON
a8 <- c(a7,function()t$north()) # 上向き
a9 <- c(a8,function()t$rotate(90)) # タートルは右向き
a10 <- sierpinski_m(t,768,6,60,a9)
plot.new()
for (i in a10) i() # この部分は手続き的なプログラム。a10の各要素を描画操作として順に実行する。
オブジェクトとは¶
ここで改めてオブジェクト指向プログラミングについて説明しておきます。オブジェクトという概念はできるだけ何にでも当てはめられるようなものですので、必然的に抽象的な概念であり、説明も抽象的なものとなります。したがってこの節の内容を実感を伴って理解できない場合、ざっと読飛ばすだけで十分であり、あとでプログラムの具体例を理解してから再読されるとよいと思います。
また以下の説明は、一番基本的なよくあるオブジェクト指向言語についてのものです。 Rの場合にはR4,R5などというオブジェクト指向のいくつかの枠組みがあり、 それぞれできることや形式が異なっています。 この資料ではR5の方法で記述しています。
オブジェクトとは自分自身の局所的なデータを備え、計算を行うものです。また、他のオブジェクトとデータをやり取りします。やり取りするデータのことをメッセージと呼びます。
例えばタートルグラフィクスのプログラムではタートルはオブジェクトであり、
タートルは$x,y$座標や向き、速度、色などの自分のデータを持っています。
例えばKoch曲線を描くプログラムにt$rotate(90)という文があります。
これはtに入っているタートルのオブジェクトにrotate(90)というメッセージを送ります。
メッセージの解釈は各オブジェクトが自分自身で行います。 RのR5ではそうではありませんが、 各オブジェクトの局所的なデータは特に指定しない限り他のオブジェクトから見たり書き換えたりすることができなくなっている場合があります。 この場合、局所的なデータを見たり書き換えたりできる場合があるといっても、それらもメッセージにより行います。 基本的には見るためあるいは書き換えるためのメッセージへの反応の仕方を記述したプログラムは、メッセージを送る側ではなく、メッセージを受けるオブジェクト側が持っています。 従って外側から見てあるオブジェクトの局所的なデータを操作しているように見えたとしても、 外側からはそれらしく見えているだけであって実際にそうなのかどうかは当該オブジェクト自身にしかわかりません。
このように、データとそれへの操作方法をまとめて定義し、それらを外から直接見られなくすることをデータ隠蔽とかカプセル化と呼びます。 このようにするとデータとそれへの操作のプログラムをまとめて取り替えることが可能になり、ソフトウェアの部品化が容易になるし、プログラマは部品の余計な内部構造まで考えなくてすみます。 この概念はプログラミング言語の発展における重要な概念の一つです(しかし先に述べたようにR5ではデータ隠蔽がされていません)。
同種のオブジェクトをまとめたものをクラス(あるいは型(type))と呼ぶ場合があります。
すなわち、クラスが同じオブジェクトは、保持している局所的データの種類と個数が同じで、メッセージへの反応の仕方を記述するプログラムも同じです。
タートルグラフィクスのプログラムでは、turtle_classを定義しています。
メッセージにはメソッドと呼ばれる処理プログラムを表す一種のタグ(荷札)がついており、メソッドごとに処理プログラムを記述します。
turtle_classではforward等がメソッドです。
クラス概念があるプログラミング言語では、局所変数やメッセージへの反応の仕方を記述するプログラムを与えてクラスを定義します。クラスを新たに定義する場合、既存クラスの記述を利用することが可能です。この機能をインヘリタンス(継承)と呼びます。
上記の説明ではオブジェクト達がメッセージをやりとりして計算を行うという見方を説明しました。しかしその場合、メソッドを函数名と捉え、メッセージを受け取るオブジェクトを各函数の最初の引数であると考えることも可能です。そのような考え方をした場合、最初の引数のオブジェクトのクラス(型)によって適用される函数(メソッド)の実体が変わってくる、ということになります。
なお、上のプログラム達ではturtle_classのメソッドを増やすことはせず、
函数を定義したり手続きを記述して描画しました。
これを、メソッドを増やすことで描画するようにすることも可能です。
Rの場合、オブジェクトのクラスをclass(-)という函数で調べることができます。
c(class(1),class(t))
マルチタートルの例: 渦¶
使用しているタートルグラフィクスのライブラリではタートルを複数同時に使うことが可能です。タートルはそれぞれオブジェクトとして実現されています。以下の例では2つのタートルを使って色が異なる2つの図形を同時に描きます。タートルを2つ生成し、left、rightという変数に代入して操作を行います。例えばleft$forward(i)とすればleftに入っているタートルにメッセージforward(i)が送られ、その操作が行われます。
plot.new()
left <- turtle_class$new() # タートル生成
left$color("red") # タートルの色をRGBで指定する。この場合は赤。
left$rotate(-90) # 左
left$up()
left$forward(160)
left$down()
right <- turtle_class$new()
right$color("blue") # 青。
right$rotate(90) # 右
right$up()
right$forward(160)
right$down()
for (i in 0:400) {
left$forward(i)
left$rotate(91)
right$forward(i)
right$rotate(89)
}
木¶
以下は深さ優先で木を描くプログラムです。
dtree <- function(t, depth, theta, length) {
t$forward(length) # 現在の方向に進める
if (depth > 1) { # 葉ではない場合
t$rotate(-theta) # 左に回転
dtree(t, depth - 1, theta, length/1.2) # 長さを一定の比率で縮める
t$rotate(2*theta) # 右に回転
dtree(t, depth - 1, theta, length/1.2)
t$rotate(-theta) # 左に回転して向きを戻す
}
t$forward(-length) # 戻る
}
plot.new()
t <- turtle_class$new() # タートル生成
t$verocity(0.0018)
t$up()
t$forward(-280) # タートルを下げる。
t$down()
dtree(t,8,15,120) # 木の描画
以下は木の分岐ごとにタートルをコピーして増やし、並列に木を描くプログラムです。但し描画の過程が見られないと差がわかりません。
brtree <-function(ts, depth, theta, length) {
ts2 <- ts
for (t1 in ts) {
t1$forward(length) # 現在の方向に進める
if (depth > 1) { # 葉ではない場合
t2 <- t1$clone()
t1$rotate(-theta) # 左に回転
t2$rotate(theta) # 右に回転
ts2 <- c(ts2,t2)
}
}
if (depth > 1) brtree(ts2, depth - 1, theta, length/1.2) # 長さを一定の比率で縮める
}
plot.new()
t <- turtle_class$new() # タートル生成
t$verocity(0.0018)
t$up()
t$forward(-280) # タートルを下げる。
t$down()
brtree(list(t),8,15,120)
2つ目の課題¶
タートルグラフィクスにより図形を描くプログラムを作成し、メール本文にコピー&ペーストしてkadai08として提出せよ。図形は自分が選んだ、あるいは創作したものとしてよい。ただし描画のプログラム部分は自分で記述すること。また、kernel restart後に提出プログラム部分のみを実行し表示を確認すること。描画した画像ファイルを添付すること。Webページのinline画像として結果が表示されている場合、ブラウザの機能で画像をファイルとして保存できる。提出先やファイル名の付け方は前回と同じである。但し画像ファイルの拡張子は適切なものとすること。
これまでに学習したプログラミングの技法以外の技法も用いてもよい。R入門のリンクを見たり、サーチエンジンでR言語などを調べれば多数の解説サイトが見つかるので、それらを参照すればさまざまなプログラミングの技法やR言語の機能を知ることが可能である。
# e81234 kadai08 課題提出用IDを書き換え
#
# ここに上のタートルグラフィクスのプログラムをコピー&ペーストする。
# そうしないと、この部分単独で動作するプログラムにならない。
#
# function 描画手続き
# 描画手続き呼び出し
ベクトル(配列)¶
様々なプログラミング言語に出てくる基本的な概念の一つである配列について説明します。 配列とは、データが入る箱が並んだものです。 Rでは、箱が1次元に並んだ配列のことをベクトル、2次元のものを行列と呼び、3次元以上のものを配列と呼びます。
並んだ箱の数を配列の大きさと言います。箱の位置を指定する数字のことを添字(index)と言います。Rのように、箱の中に入る物は同じ種類の基本的なデータしか許していない言語もあります。類似のデータ型として、Rでは箱ごとに様々な種類のデータを入れられるリストもあります。例えばリストの中に配列、リストを入れることも可能です。
(a <- c(1,3,5,7,9)) # 最初の要素が1、2番目の要素が3...という大きさ5の配列
c(length(a), typeof(a)) # ベクトルの大きさと型。この場合型を合わせるため、整数5が文字型に変換される。
(b <- list(1,3,5,7,9)) #こちらはリスト
c(1,3,5,7,9)というのは最初の要素が1、2番目以下の要素が3,5...という大きさ5のベクトルで、上の文によりaという変数に代入されます。
Rでは基本的なデータが実は全てベクトルであり、typeof(a)がdouble(倍精度浮動小数点数)だというのは、
aの型が通常の他の言語における一つの浮動小数点数だというのではなく、
それのベクトルだということを言っています。
c <- 10
typeof(c) # cの型は一つの浮動小数点数のように思えるが、実は長さ1のベクトル
添字が1から始まるかそうでなかの違いを除き、他のプログラミング言語の場合とほぼ同様に以下のようになります。
c(a[1],a[4]) # 添え字は1から始まる
a[1] <- 10
a
c[1] # cがベクトルである証拠。
Rのリストによりスタックやキューを実現できる¶
(a <- list(1, 2, 3, 4, 5)) # リストを作成し、aに代入する。
length(a) # aの長さ
a[[length(a)+1]] <- 6 # リストの大きさを1増やし、最後にデータを追加する。
a # リストでは[]の代わりに[[]]を用いる。この場合ベクトルでも動作する。
a[[1]] <- NULL # リストの最初のデータを取り除く。入れたデータを順に取り出す仕組みをキューと呼ぶ。
a # これはベクトルでは動作しない。
上の操作によりリストをキューとして使えます。今の場合には、最初1,2,3,4,5というデータがこの順にキューに入っていたところ、最後に6というデータを追加し、その後キューから最初のデータである1を取り出しました。
a[[length(a)]] <- NULL # リストの最後のデータを取り除く
a
入れたデータを逆順に取り出す仕組みをスタックと呼びます。上の操作によりリストををスタックとして使えます。
リストとベクトルのいろいろな操作¶
a <- c(1, 2, 3, 4)
b <- c(5, 6, 7, 8)
c(a,b) # 2つのベクトルを結合する。1つ以上がリストであっても動作する。その場合の結果はリスト。
Rではリストやベクトルを実引数として渡すといわゆる値渡しとなるため、 それの要素を変更しても呼び出し側には反映されません。
x <- c(1,2,3)
y <- list(4,5,6)
test1 <- function(x) {
x[2] <- 0 # 仮引数xは局所変数で、ベクトルxが値渡しなのでyの中身を変更してもxに影響しない。
x
}
test2 <- function(x) {
x[2] <- NULL # 仮引数xは局所変数で、リストyが値渡しなのでxの中身を変更してもyに影響しない。
x
}
test1(x)
x
test2(y)
y
函数定義の中で代入に<<-を使わず、他の大域変数を更新する函数呼び出しを行わなければ、その函数の呼び出しにより大域変数が更新されることは通常ありません。
例題: エラトステネスの篩¶
ここでは配列を使った例題として、エラトステネスの篩(ふるい)と呼ばれる手法により、ある数までの素数をすべて求めてみます。以下がそのプログラムです。値0で数値を消したことを表しています。
n <- 300
a <- 1:n
a[1] <- NA # 1からnまでの数のベクトルの、1に対応する最初の要素をNA(欠損データ)にする。
for (i in a) { # 通常はデータがないことを表す。この場合は素数でないことを表している。
if (!is.na(i) && 2*i <= n) { # NA以外の場合。2*i <= nはRのseqの仕様のためのチェック。
for (j in seq(2*i,n,i)) { # i以外のiの倍数を消す。最後のiはjをiずつ増やすことを指定している。
a[j] <- NA
}
}
}
# for文の部分はmapplyを使うと次のようにも書ける。a_はダミー。
# mapplyは、第二引数の配列の各要素に函数を適用した結果の配列を作って返す。
# <-を<<-とせねばならないことに注意。<-としたのではaが局所変数の扱いとなる。
# a_ <- mapply(function(i){if(!is.na(i) && 2*i <= n){for (j in seq(2*i,n,i)) a[j] <<- NA}},a)
i <- 0
b <- c() # 空ベクトル。 aの各要素に対し、それがNA以外の時のみbに入れる。
a_ <- mapply(function(x){if (!is.na(x)) b[(i <<- i + 1)] <<- x},a) # a_は結果非表示のためのダミー。
b
このプログラムでは、最初に1つNA(欠損値)があり、その後2以上与えられた数までの数値を要素として持つベクトルを2行目で作っています。この時点では、1は素数でなく、素数だとわかっているのは2だけで、3以降は素数である可能性がある数値がベクトル中に残っている状態です。ある添字の要素がNAでなければその添字の値自身がその添字の要素として入っています。
4-10行目で、ベクトルの各要素について、それがNAでなければその数の2倍の添字位置からベクトルの最後までの、その数の倍数の添字位置の要素をNAに置き換えるという操作を繰り返し行います。ここではループが2重になっていることに注意してください。
下から2行目のmapplyはmap函数と呼ばれるもので、内包表記に近い書き方ができます。
合成数の位置に入っているNAを除いたベクトルを作っています。
3つ目の課題¶
3つ目のkadai09はオプションです。即ち、提出したい人だけが提出してください。
先の節である数nまでの素数をすべて求める方法を見てみました。今度はまず、ある数までの素数の表を求め、それを使って数mを素因数分解する函数factorを書いてください。mは、函数の引数として与えるようにしてください。また、出力の形式は以下のようなものとしてください。
[[素因数1, 個数1], [素因数2, 個数2], … ,[素因数k, 個数k]]素因数iの個数i乗をi=1,...,kについてすべて掛け合わせた結果がmとなります。また、個数iは1以上の自然数です。ただし、あらかじめ求めた素数の表が、mの分解に足りない場合には、その旨を出力するようにしてください。その場合、途中まで行える分解の結果も表示してください。
例えば[2,3,5,7]という素数の表を求めていた場合、53の素因数分解には7*7 < 53なので表が足りません。63の分解であれば3で2回割り切れて7となりますので分解できます。3339=3*3*7*53の分解は、3で2回割って7で割ると53となり、7*7<53なので表が足りませんが、[[3,2],[7,1],[53,1]]というところまでは分解できます。ただしこの場合には最後の53が素数かどうかはわからないということになります(今の場合にはたまたま素数です)。表が足りない場合には、素数かどうかわからない部分も指示するようにしてください。例えば「[[3,2],[7,1],[53,1]](ただし最後の因数は素数とは限りません)」などと出力すれば十分です。
これまでに学習したプログラミングの技法以外の技法を用いても構いません。
# e81234 kadai09
#
# factor <- function(m)